|
|
|
|
|
|
3.3 Produktcontrolling |
|
3.3.5 Produktcontrolling: Gewinnschwellenanalyse |
Mkt 3352 [3/4] |
|
|
c) Rechnerische Lösung |
Für die rechnerische Bestimmung der produkt- bzw.
auftragsbezogenen Gewinnschwelle können folgende
Ansätze genutzt werden:1
Der Break-even-Point ist auch in diesem Falle jener
Punkt, an dem die Erlöse E genau den
Gesamtkosten K entsprechen:
Erlöse E = Kosten K = Fixkosten FK + variable
Kosten vK. (1)
Für die Erlöse
E und die Kosten K gelten
folgende Bestimmungsgleichungen:
Erlöse E [EUR] =
Preis P [EUR/ME] * Absatzmenge x [ME],
(2)
Kosten K [EUR] = Fixkosten fK [EUR] + variable
Stückkosten vk [EUR/ME] * Absatzmenge x [ME]. (3)
Da bei der Gewinnschwelle nach Gleichung (1) die
Beziehung E = K gilt, folgt mit
Bezugnahme auf die Gleichungen (2) und (3):
P * x0 = fK + vk * x0
(4).
Wird diese Gleichung nach der Größe
x0 umgestellt, erhalten wir
folgende Bestimmungsgleichung für die
Ermittlung der produkt- bzw. auftragsbezogenen
Gewinnschwelle:
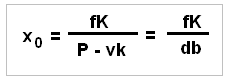
Es bedeuten:
x0
Break-even-Menge [ME],
fK
Fixkosten des Unternehmens [EUR],
P
Verkaufspreis [EUR/ME],
vk
variable Stückkosten [EUR/ME],
db
Stück-Deckungsbeitrag [EUR/ME] ("kleiner" DB) mit
db = P ./. vk.
|
Im betrachteten Fallbeispiel erhalten wir aufgrund der
gegebenen Daten für die Fixkosten fK
[EUR], den Verkaufspreis P [EUR/ME] und
die variablen Größe vk [EUR/ME] folgendes
Resultat für die produktbezogene Gewinnschwelle:
x0 = 504.000 EUR / (2.800 EUR/ME] ./.
1.540 [EUR/ME] = 504.000 / 1.260 = 400 ME.
Damit wird das Ergebnis der graphischen Lösung
präzisiert. |

|
|
1
Siehe hierzu: |
|
von KÄNEL, S.: Lernsoftware "Controlling".
NWB-Verlag, Herne 2009. |
|
ZIEGENBEIN, K.: Controlling.
NWB-Verlag, Herne 2012. |
|
|
|
|
|
|
|