|
|
|
|
|
|
3.3 Produktcontrolling |
|
3.3.5 Produktcontrolling: Gewinnschwellenanalyse |
Mkt 3351 [2/4] |
|
|
b) Graphische Lösung |
Für die graphische Lösung wählt der Planungsrechner ein
x,y-Diagramm, wobei auf der x-Achse
die zu ermittelnde Absatzmenge (Symbol x
[ME]) und auf der y-Achse die
Umsatzerlöse E [EUR] sowie die Fixkosten
fK [EUR], die variablen Kosten vK
[EUR] und die Gesamtkosten K [EUR]
abgetragen werden.
Die Erlöskurve E = f (x
) ist - unter der Annahme eines konstanten
Preises P [EUR/ME] eine Gerade mit dem
Anstieg P.
Die Fixkostenkurve
fK = f (x) ist eine Parallele zur
x-Achse, während die Kurve der variablen Kosten
vK = f (x) als eine Gerade mit dem
Anstieg von vk in das Diagramm
einzutragen ist.
Die Gesamtkostenkurve K =
f x) beginnt bei x = 0 Mio. EUR
auf der y-Achse beim Wert der Fixkosten
fK und verläuft dann im Weiteren parallel
zur Kurve der variablen Kosten.
Die
Gewinnschwelle (= Break-even-Point) ist
jener Punkt im x, y - Diagramm, bei dem die
Gesamtkostenkurve K = f (x) die
Erlöskurve E = f (x) schneidet, denn hier
gilt Erlöse E = Kosten K (siehe
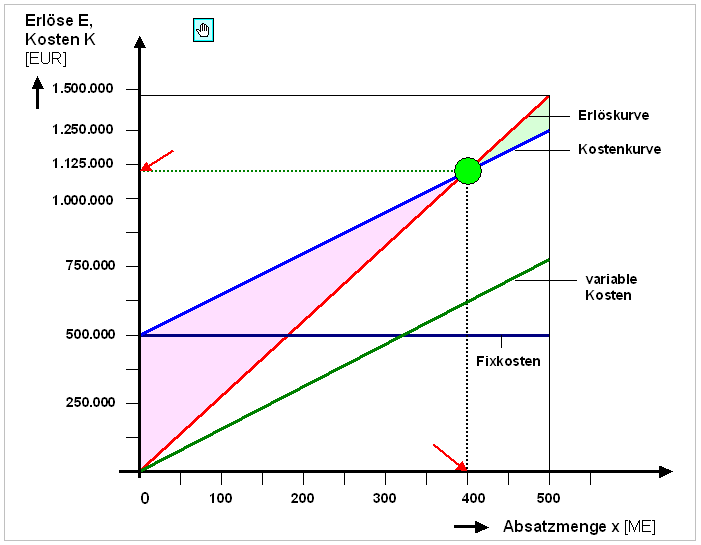
Bild 3.30). |
 |
|
Bild 3.30: Gewinnschwellenanalyse (graphische Lösung) |
Die Gewinnschwellenwerte sind auf der x-Achse
dort abzulesen, wo ein Lot vom Break-even-Point die
x-Achse schneidet.
Es kann im
betrachteten Beispiel der Wert x = 400 ME
abgelesen werden. Die mit
dieser Absatzmenge verbundenen Erlöse E
und Kosten K sind auf der y-Achse
dort abzulesen, wo eine in Höhe des Break-even-Points
gezogene Gerade die y-Achse scheidet.
Es können die Werte E = K knapp unter
der Markierung von E = K = 1.125.000 EUR
abgelesen werden.
Die Grafik verdeutlicht aber
zugleich das Problem der Ermittlung einer
produkt- bzw. auftragsbezogenen Gewinnschwelle, denn:
- Was ist, wenn die konkrete Nachfrage nach
dem Erzeugnis P-X100 bestenfalls bei
x = 250 ME liegt oder
- was ist, wenn die für das ErzeugnisP-X100
einsetzbare Produktionskapazität eine
Produktionsmenge von nur x = 300 ME
erlaubt?
Daraus ergibt sich die Frage: Wenn das Erzeugnis P-X
100 mit den angegebenen Parametern aus anderen
Gründen dennoch in das Absatzprogramm aufgenommen werden
soll, wie kann dann eine Break-even-Menge unterhalb von
400 ME erreicht werden?
Antworten
hierzu liefert die rechnerische Lösung
zur gestellten Aufgabe. |

|
|
1
Siehe hierzu: |
|
von KÄNEL, S.: Lernsoftware "Controlling".
NWB-Verlag, Herne 2009. |
|
ZIEGENBEIN, K.: Controlling.
NWB-Verlag, Herne 2012. |
|
|
|
|
|
|
|